Conway's Game of Life
As a geeky teenager navigating the vast landscape of computer science and mathematics, it’s not uncommon to stumble upon mind-bending puzzles and intricate algorithms that pique our curiosity. One such fascinating discovery is Conway’s Game of Life, an intriguing cellular automaton that captivates the minds of young tech enthusiasts. Developed by the brilliant mathematician John Horton Conway, this simple yet powerful concept has become a playground for exploration and experimentation for many geeky teenagers.

"If experimenters have free will, then so do elementary particles." - John Horton Conway
The Basics of Conway’s Game of Life
Conway’s Game of Life is a zero-player game, meaning it requires no further input once the initial state is set. It consists of a grid of cells, each having two possible states: alive or dead. The rules that govern the evolution of these cells are deceptively simple but lead to complex and mesmerizing patterns.
The Rules of Life
The Game of Life follows a set of simple rules that govern the behavior of its cellular automaton. These rules determine how each cell in the game’s grid evolves from one generation to the next. Here are the fundamental rules of the Game of Life: Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent.
- Any live cell with fewer than two live neighbors dies, as if by underpopulation.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by overpopulation.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
These four rules elegantly dictate the life and death of each cell, creating a dynamic system that unfolds over time.
By applying these rules simultaneously to every cell in the grid, the Game of Life progresses from one generation to the next, creating visually stunning and intricate patterns. Each cell’s state is updated based on the states of its neighboring cells, leading to a dynamic and evolving system.
"In Conway's Game of Life, chaos emerges from order."
Patterns: Geeky Art in Motion
It’s time to geek out over the mind-boggling patterns that emerge within the Game of Life. I’ll use p5.js to implement this.
The algorithm for Conway’s Game of Life can be summarized in the following steps:
- Create an initial grid: Set up a two-dimensional grid of cells, where each cell can be in one of two states: alive or dead. This initial configuration serves as the starting point for the game.
function make2DArray(rows, cols){
let arr = new Array(rows);
for(let i=0; i<rows; i++){
arr[i] = new Array(cols);
}
return arr;
}
- Iterate over the grid: For each cell in the grid, apply the rules to determine its state. To apply these rules, count the number of live neighbors for each cell. Neighbors include the eight cells adjacent to the current cell (horizontal, vertical, and diagonal). Based on the current state and the number of live neighbors, determine the cell’s state in the next generation.
function countNeighbours(grid, x,y){
let alivenbrs = 0;
for(let i=-1; i<2; i++){
for(let j=-1; j<2; j++){
if(i==0 && j==0){
continue;
}
let rx = ((x+i)%rows + rows)%rows;
let ry = ((y+j)%cols + cols)%cols;
if (grid[rx][ry]>=1){alivenbrs = alivenbrs + 1;}
}
}
return alivenbrs;
}
- Update the grid: Once all cells have been evaluated and their next states determined, update the grid to reflect the new generation. Set each cell’s state according to the rules applied in the previous step.
function updateCell(i,j){
let liveNB = countNeighbours(grid, i,j);
let curr_state = grid[i][j];
let new_state = curr_state;
if(curr_state <= 0 && liveNB == 3){
new_state = 1;
}
else if(curr_state<=0){
new_state -= 1;
}
else if (curr_state>=1 && (liveNB<2 || liveNB >3)){
new_state = 0;
}
else if (curr_state>=1){
new_state += 1;
}
return new_state;
}
- Repeat: Iterate through the grid, applying the rules and updating the states of cells to create subsequent generations. Continue this process indefinitely or until a specific termination condition is met.
function gameOfLife(){
let temp_curr;
let temp_prev;
let temp_0;
for(let i=0; i<rows; i++){
temp_curr = new Array(cols).fill(0);
for(let j=0; j<cols; j++){
temp_curr[j] = updateCell(i,j);
//new_grid[i][j] = updateCell(i,j);
}
if(i>1){
grid[i-1] = temp_prev;
}
temp_prev = temp_curr;
if(i==0)
temp_0 = temp_curr;
}
grid[rows-1] = temp_prev;
grid[0] = temp_0;
}
Please checkout the demo and github code here.
Glider Guns
Conway’s Game of Life also allows for the construction of various logical components. Glider guns, for example, are structures that continually generate gliders, which can be thought of as moving signals. These glider guns can be used to create logic gates such as AND, OR, and NOT gates, forming the building blocks of more complex computational systems within the game.
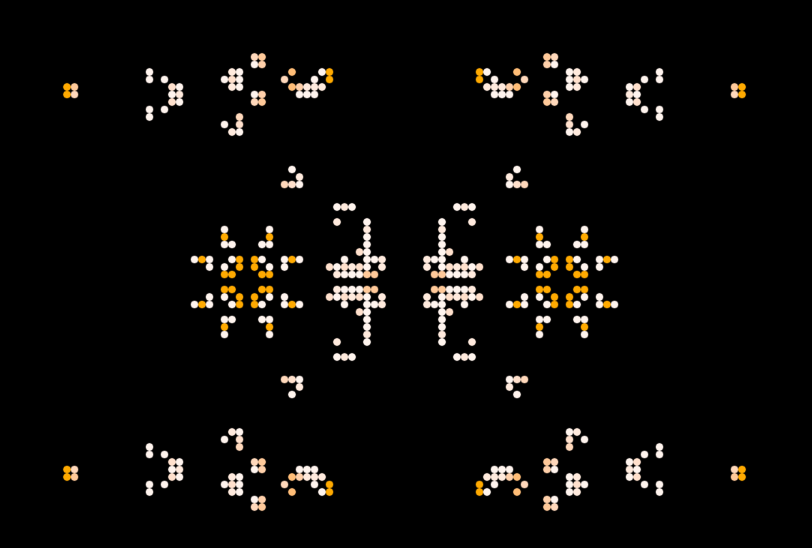
Complexity and Universality of the Game
The Game of Life possesses both complexity and universality, making it a fascinating subject in the realm of computational theory. Let’s explore these concepts in more detail:
The Emergence of Complexity
Despite its simple set of rules, Conway’s Game of Life exhibits a stunning level of complexity. From the interplay of live and dead cells, intricate patterns emerge, ranging from stable structures to oscillators, gliders, and even self-replicating entities. The game’s evolution unfolds dynamically, showcasing the potential for endless possibilities within a finite set of rules.
Universality: Turing Completeness
One of the most astonishing aspects of Conway’s Game of Life is its universality, specifically its ability to simulate any Turing machine. A Turing machine is a theoretical model of computation that can solve any problem that can be computed algorithmically. By constructing specific configurations within the game, it is possible to create structures that mimic the behavior of a Turing machine, effectively transforming the Game of Life into a computational device capable of solving complex problems.
In summary, the Game of Life embodies both complexity and universality. Its simple rules give rise to intricate and visually stunning patterns, demonstrating the inherent complexity that can emerge from simplicity. Moreover, its ability to simulate any other computational system showcases its universality, illustrating the vast computational power that can be harnessed within this seemingly simple cellular automaton.
Enjoy Reading This Article?
Here are some more articles you might like to read next: